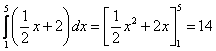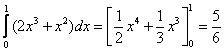Aufgabe 1:

Gegeben ist die Funktion .

(a) Berechne die Gleichung der Tangenten an den Graphen von an der Stelle

(b) Zeige durch Rechnung, dass die Punkte und auf dem Graphen von liegen. Berechne die Gleichung der Sekante durch die Punkte und .

(c) Zur Sekante existiert eine parallele Tangente an den Graphen. Berechne den Berührpunkt dieser Tangente an den Graphen.

(d) Berechne die Normale zur Tangente durch den Berührpunkt aus Aufgabenteil (c).

Lösung:

(a)

Allgemeine Geradengleichung:

Steigung der Tangente an der Stelle ist der Wert der 1. Ableitung an der Stelle .

y-Achsenabschnitt wird durch einsetzen und auflösen der Geradengleichung bestimmt.

Aus und

und somit ist die Geradengleichung der Tangente an den Graphen an der Stelle

.

(b)

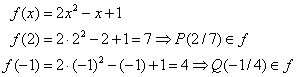
Berechnung der Sekante durch und als Gleichungssystem mit 2 Gleichungen und 2 Unbekannten

allgemeine Geradengleichung muss von den Punkten und erfüllt werden:

und

Auflösen der zweiten Gleichung nach liefert , dieses in die erste Gleichung eingesetzt, ergibt folgende Gleichung:

Dieses Ergebnis eingesetzt in die Gleichung liefert und somit lautet die gesuchte Sekantengleichung:

(c)

Die parallele Tangente muss die selbe Steigung wie die errechnete Sekante aus (b) haben.

Somit hat der Graph von an der Stelle eine Tangente mit der Steigung von . Der Berührpunkt hat die Koordinaten und und lautet

.

(d)

Die Steigung der Normalen zum Punkt an den Graphen errechnet sich wie folgt aus der Steigung der Tangenten (Normale und Tangente stehen orthogonal aufeinander):

.

Nun muss die Normale folgender Gleichung genügen und den Punkt beinhalten

.

Hieraus folgt die gesuchte Normalengleichung:

.

Aufgabe 2:

Die Funktion mit schneidet die y-Achse bei und geht durch den Punkt . Die Tangente an den Berührpunkt hat die Steigung -2.

Wie lautet die Funktion?

Lösung:

Die Funktion hat 3 Unbekannte, somit sind 3 Gleichungen nötig diese Unbekannten zu finden.

(i) aus der Information „schneidet die y-Achse bei “ folgt:

(ii) aus der Information „geht durch den Punkt “ folgt:

(iii) aus der Information „Die Tangente an den Berührpunkt hat die Steigung -2.“ folgt:
mit folgt

Nun sind nur noch die Gleichungen und zu lösen und man erhält und :

löst man die Gleichung nach auf erhält man , dieses nun in die Gleichung eingesetzt, liefert:

.

Dieses Ergebnis kann man in einsetzen und man erhält

.

Und so erhält man die gesuchte Funktion:

.

Aufgabe 3:

Mit einem Zaun von der Länge 100m soll ein rechteckiger Hühnerhof mit möglichst großem Flächeninhalt eingezäunt werden. Bestimme die Länge und die Breite des Hofs und gib den Flächeninhalt an.

Lösung:

Extremalbedingung:

Nebenbedingung:

Zielfunktion:

Die Suche nach dem Maximum der Funktion ergibt:

Aufgabe 4:

Berechne folgende Integrale:

(a)

(b)

(c)

Lösung:

(a)

(b)

(c)

Aufgabe 5:

Bestimme zunächst die Nullstellen von und skizziere den Graphen. Berechne den Inhalt der Fläche, die der Graph mit der x-Achse einschließt.

Lösung:

Nullstellen: