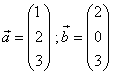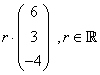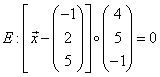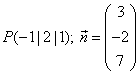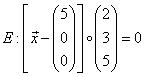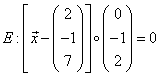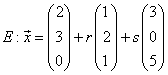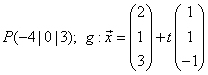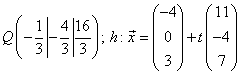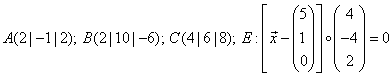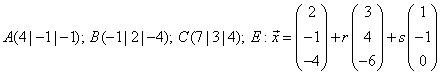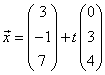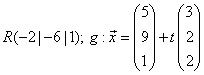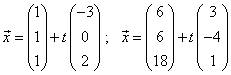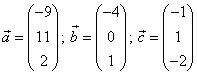Aufgabe 2:
Bestimme alle Vektoren, die zu 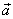 und
und 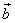 orthogonal sind.
orthogonal sind.
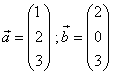
Lösung:
Aufgabe 3:
Gib eine Koordinatengleichung der Ebene 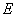 an.
an.
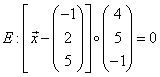
Lösung:
z.B.: 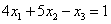
Aufgabe 4:
Gib eine Koordinatengleichung der Ebene an, für die gilt: Die Ebene geht durch den Punkt 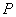 und hat den
Normalenvektor
und hat den
Normalenvektor 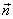 .
.
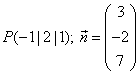
Lösung:
z.B. 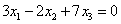
Aufgabe 5:
Bestimme für die Ebene 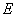 eine Gleichung in
Normalenform.
eine Gleichung in
Normalenform.
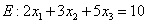
Lösung:
z.B. 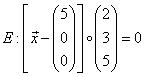
Aufgabe 6:
Die Ebenen 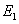 und
und 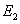 sollen zueinander
orthogonal sein. Bestimme den Parameter
sollen zueinander
orthogonal sein. Bestimme den Parameter 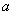 in der Gleichung von
in der Gleichung von 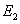 so, dass dies der Fall
ist.
so, dass dies der Fall
ist.
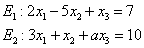
Lösung:
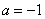
Aufgabe 7:
Gegeben sind zwei Punkte  und
und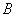 und eine Ebene
und eine Ebene 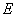 . Bestimme eine Gleichung der Ebene
. Bestimme eine Gleichung der Ebene 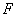 , für die gilt:
, für die gilt: 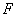 geht durch dir Punkte
geht durch dir Punkte 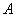 und
und 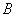 und ist zur Ebene
und ist zur Ebene 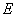 orthogonal.
orthogonal.
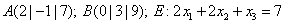
Lösung:
z.B. 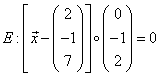
Aufgabe 8:
Eine Gerade 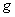 durch
durch 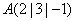 ist orthogonal zur
Ebene
ist orthogonal zur
Ebene 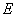 . Bestimme eine Gleichung von
. Bestimme eine Gleichung von 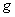 .
.
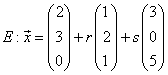
Lösung:
z.B. 
Aufgabe 9:
Gegeben sind ein Punkt 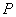 und eine Gerade
und eine Gerade 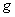 .Bestimme den Punkt
.Bestimme den Punkt 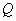 auf
auf 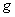 so, dass die Gerade
so, dass die Gerade 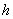 durch
durch 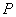 und
und 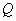 orthogonal zu
orthogonal zu 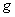 ist. Gib auch eine
Gleichung für
ist. Gib auch eine
Gleichung für 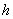 an.
an.
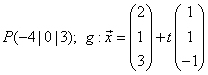
Lösung:
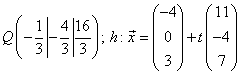
Aufgabe 10:
Berechne die Abstände der Punkte 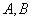 und
und 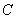 von der Ebene
von der Ebene 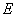 .
.
(a) 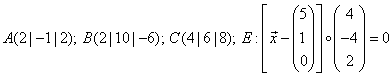
(b) 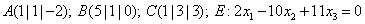
(c) 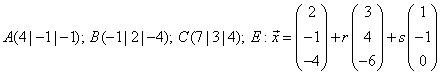
Lösung:
(a) 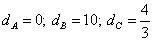
(b) 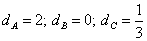
(c) 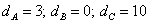
Aufgabe 11:
Berechne die Abstände der Punkte 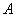 ,
, 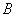 und
und 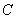 von der Ebene durch
die Punkte
von der Ebene durch
die Punkte 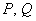 und
und 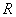 .
.
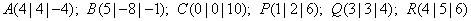
Lösung:
Ebenegleichung:
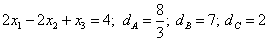
Aufgabe 12:
Gegeben sind die Ebene 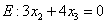 und der Punkt
und der Punkt 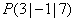 .
.
(a) Stelle
eine Gleichung der Geraden 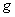 auf, die orthogonal
zur Ebene
auf, die orthogonal
zur Ebene 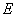 ist und durch den
Punkt
ist und durch den
Punkt 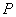 geht.
geht.
(b) Bestimme
den Lotfußpunkt, d.h. den Schnittpunkt 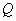 der Geraden
der Geraden 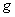 mit der Ebene
mit der Ebene 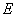 . Berechne den Abstand der Punkte
. Berechne den Abstand der Punkte 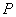 und
und 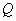 .
.
(c) Berechne
direkt den Abstand von 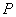 zur Ebene
zur Ebene 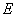 . Kontrolliere damit das Ergebnis von 12 (b).
. Kontrolliere damit das Ergebnis von 12 (b).
Lösung:
(a) z.B.
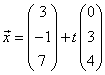
(b) 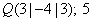
(c) 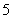
Aufgabe 13:
Die Menge aller Punkte , die zu einer Ebene 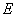 einen festen Abstand
haben, bilden zwei zu
einen festen Abstand
haben, bilden zwei zu 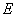 parallele Ebenen
parallele Ebenen 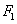 und
und 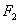 . Bestimme die Gleichungen der Ebenen
. Bestimme die Gleichungen der Ebenen 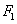 und
und 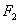 so, dass
so, dass 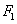 und
und 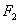 von
von 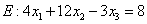 den Abstand 2 haben.
den Abstand 2 haben.
Hinweis: Wähle einen günstigen Punkt, z.B. einen Punkt auf der 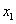 -Achse. Bestimme dann seine Koordinaten so, dass sein Abstand
von der Ebene
-Achse. Bestimme dann seine Koordinaten so, dass sein Abstand
von der Ebene 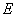 gerade 2 beträgt (zwei
Lösungen).Die gesuchten Ebenen gehen durch diese Punkte und sind parallel zu
gerade 2 beträgt (zwei
Lösungen).Die gesuchten Ebenen gehen durch diese Punkte und sind parallel zu 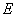 .
.
Lösung:
Punkte auf der 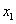 -Achse:
-Achse: 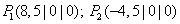
Ebenengleichungen: 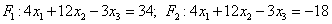
Aufgabe 14:
Berechne den
Abstand des Punkte 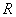 von der Geraden
von der Geraden 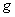 .
.
Lösung:
11
Aufgabe 15:
Berechne den
Flächeninhalt des Dreiecks 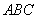 .
.
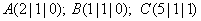
Lösung:
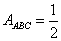
Aufgabe 16:
Berechne den
Abstand zwischen den Geraden mit den Gleichungen
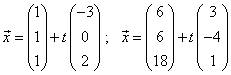
Lösung:
Aufgabe 17:
Bestimme die
Zahlen 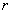 und
und 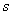 so, dass
so, dass 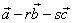 orthogonal zu
orthogonal zu 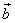 und zu
und zu 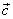 ist.
ist.
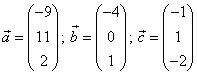
Lösung:
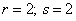
Aufgabe 18:
Berechne das
Volumen der Pyramide mit den Eckpunkten 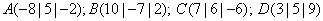
Lösung:
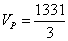
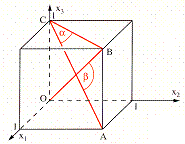 Aufgabe 1:
Aufgabe 1:![]() zwischen den
Flächendiagonalen
zwischen den
Flächendiagonalen ![]() und der Raumdiagonalen
und der Raumdiagonalen
![]() .
.![]() zwischen den
Raumdiagonalen
zwischen den
Raumdiagonalen ![]() und
und ![]() ?
?