Hinweis zur Bearbeitung der Aufgaben:

• Aufgabe 1-9 sind Basisaufgaben (Überprüfung des Grundwissens)
• Aufgabe 10-16 sind komplexe Aufgaben, welche mehrere Methoden kombinieren.
• Aufgaben 17 & 18 sind Aufgaben, welche bestimmtes Wissen abfragen.
• Der Umfang der Aufgaben entspricht nicht der Klausur :)
• Die Aufgaben prüfen alle Themengebiete der Klausur ab, jedoch werden die Klausraufgaben deutlich anders „aussehen“. ;)

Aufgabe 1:

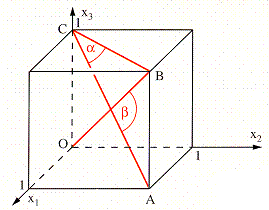
(a) Bestimme anhand der nebenstehenden Zeichnung die Größe des Winkels zwischen den Flächendiagonalen und der Raumdiagonalen .

(b) Wie groß ist der Winkel zwischen den Raumdiagonalen und ?

Aufgabe 2:

Bestimme alle Vektoren, die zu und orthogonal sind.

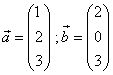
Aufgabe 3:

Gib eine Koordinatengleichung der Ebene an.

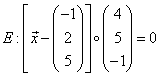
Aufgabe 4:

Gib eine Koordinatengleichung der Ebene an, für die gilt: Die Ebene geht durch den Punkt und hat den Normalenvektor .

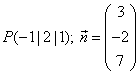
Aufgabe 5:

Bestimme für die Ebene eine Gleichung in Normalenform.

Aufgabe 6:

Die Ebenen und sollen zueinander orthogonal sein. Bestimme den Parameter in der Gleichung von so, dass dies der Fall ist.

Aufgabe 7:

Gegeben sind zwei Punkte und und eine Ebene . Bestimme eine Gleichung der Ebene , für die gilt: geht durch dir Punkte und und ist zur Ebene orthogonal.

Aufgabe 8:

Eine Gerade durch ist orthogonal zur Ebene . Bestimme eine Gleichung von .

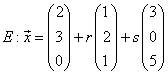
Aufgabe 9:

Gegeben sind ein Punkt und eine Gerade .Bestimme den Punkt auf so, dass die Gerade durch und orthogonal zu ist. Gib auch eine Gleichung für an.

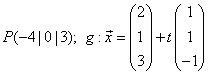
Aufgabe 10:

Berechne die Abstände der Punkte und von der Ebene .

(a)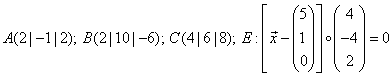

(b)

(c)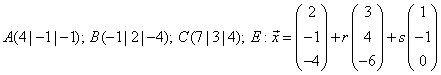

Aufgabe 11:

Berechne die Abstände der Punkte , und von der Ebene durch die Punkte und .

Aufgabe 12:

Gegeben sind die Ebene und der Punkt .

(a) Stelle eine Gleichung der Geraden auf, die orthogonal zur Ebene ist und durch den Punkt geht.

(b) Bestimme den Lotfußpunkt, d.h. den Schnittpunkt der Geraden mit der Ebene . Berechne den Abstand der Punkte und .

(c) Berechne direkt den Abstand von zur Ebene . Kontrolliere damit das Ergebnis von 12 (b).

Aufgabe 13:

Die Menge aller Punkte , die zu einer Ebene einen festen Abstand haben, bilden zwei zu parallele Ebenen und . Bestimme die Gleichungen der Ebenen und so, dass und von den Abstand 2 haben.

Hinweis: Wähle einen günstigen Punkt, z.B. einen Punkt auf der -Achse. Bestimme dann seine Koordinaten so, dass sein Abstand von der Ebene gerade 2 beträgt (zwei Lösungen).Die gesuchten Ebenen gehen durch diese Punkte und sind parallel zu .

Aufgabe 14:

Berechne den Abstand des Punkte von der Geraden .

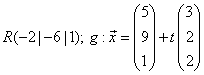
Aufgabe 15:

Berechne den Flächeninhalt des Dreiecks .

Aufgabe 16:

Berechne den Abstand zwischen den Geraden mit den Gleichungen

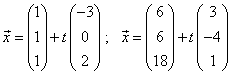
Aufgabe 17:

Bestimme die Zahlen und so, dass orthogonal zu und zu ist.

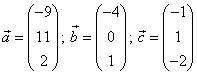
Aufgabe 18:

Berechne das Volumen der Pyramide mit den Eckpunkten