Aufgabe 1:

Ein langes, breites und tiefes Schwimmbecken wird gefüllt. Pro Stunde fließen Wasser zu.

(a) Gib die Funktion Fülldauer (in h) Wassertiefe (in m) an.

(b) Welche Wassertiefe ist nach 3 Stunden erreicht?

(c) Wie lange dauert es, bis das Becken bis 20cm unter den oberen Rand gefüllt ist.

Lösung:

Wasser stehen in dem Becken hoch.

(a)

(b) 0,48

(c) gibt 11,25h

Aufgabe 2:

(a) Zeige, dass die folgenden Gleichungen nicht bei allen linearen Funktionen erfüllt sind:
für alle .

(b) Für welche linearen Funktionen sind diese Gleichungen erfüllt.

Lösung:

(a) Es sei . Aus erhält man die Bedingung .
Aus .

(b) Nur Proportionalitäten sind die Gleichungen erfüllt.

Aufgabe 3:

Ein Sparguthaben von 5000€ liegt 10 Jahre auf der Bank, ohne dass jemals Geld abgehoben wird. Es verzinst sich mit 6% jährlich.

(a) Wie groß ist der Wachstumsfaktor, mit dem das Guthaben anwächst?

(b) Wie hoch ist das Guthaben 6Jahren und wie hoch nach x Jahren?

Lösung:

(a) 1,06

(b)

Aufgabe 4:

Gib den Funktionsterm von an. Beachte die Definitionsmenge.

(a)

(b)

(c)

Lösung:

(a)

(b)

(c)

Aufgabe 5:

(a) Bei manchen Folgen ist es zweckmäßig, statt der Differenz den Quotienten zu betrachten. Wie zeigt sich an ihm, dass die Folge monoton ist?

(b) Untersuche mittels des Quotienten die Folgen 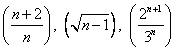und auf Monotonie.

Lösung:

(a)

(b)

Aufgabe 6:

Untersuche, ob die Folge sowohl monoton als auch beschränkt ist.

(a)

(b)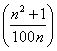

(c)

(d)

Lösung:

(a) monoton zunehmend,

(b) monoton zunehmend, nach oben unbeschränkt,

(c) monoton abnehmend,

(d) monoton abnehmend,

Aufgabe 7:

Ist die Folge nach oben oder unten beschränkt? Wie ist das Monotonieverhalten?

(a)

(b)

Lösung: (prosaische Lösung, weitere Argumentationslinien vorstellbar!)

(a) Zur besseren Vorstellung welche Werte von der Folge ausgegeben werden, die ersten 10 Folgewerte:
:
Monotonieverhalten: Überlegung ist weder monoton zunehmend noch monoton abnehmend:
Beweis durch Widerspruch:
(1) Annahme: sei monoton zunehmend, dann gilt:
; für gerade wird das -te
Folgendglied immer kleiner (=0) als das -te Folgenglied.
WIDERSPRUCH!
(2) Annahme: sei monoton abnehmend, dann gilt:
; für ungerade wird das -te
Folgendglied immer kleiner (=0) als das -te Folgenglied.
WIDERSPRUCH!
Die Folge ist weder monoton zunehmend, noch monoton abnehmend und es gilt: die Folge besitzt nur eine untere Schranke ().

(b) Zur besseren Vorstellung welche Werte von der Folge ausgegeben werden, die ersten 10 Folgewerte:
:
Untersuchung der Folge: zerlegt man die Folge in zwei Faktoren, dann erkennt man schnell, dass für gerade und ungerade jeweils wechselnde Vorzeichen erzeugt und der Faktor für wachsende unbegrenzt wächst.
ist nicht monoton
ist nicht beschränkt, weder nach oben, noch nach unten.