Bearbeitungszeit: 90Minuten zugelassene Hilfsmittel: Taschenrechner

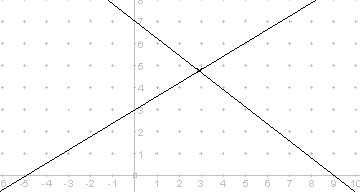
Aufgabe 1:

Berechne die Koordinaten des Schnittpunktes der beiden Geraden und gib den Schnittwinkel der beiden Geraden an.

Lösung:

Geradengleichungen bestimmen (durch ablesen der Koordinaten der Achsenschnittpunkte):
steigende Gerade: Schnittpunkte -Achse und - Achse
(direkt Funktionsgleichung angeben)
(Steigung und -Achsenabschnitt ist ablesbar!)

fallende Gerade: Schnittpunkte -Achse und - Achse

Schnittpunktbestimmung durch gleichsetzen der beiden Geradengleichungen:
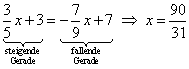und diese Koordinate in eine der beiden Geradengleichungen eingesetzt, ergibt folgende -Koordinate des Schnittpunktes:
.
Den Schnittwinkel der beiden Geraden wird mittels dem jeweiligen Steigungswinkel der Geraden (gegenüber der -Achse) bestimmt.

Es gilt: .

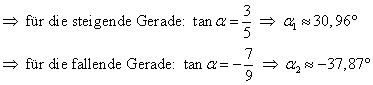
Aufgabe 2:

Gegeben ist das Dreieck mit .

(a) Gib den Flächeninhalt des Dreiecks an.

(b) Ergänze das Dreieck zu einem Parallelogramm und gib die Koordinaten des Punktes an.

Lösung:

(a) Skizze:










Flächeninhalt Dreieck 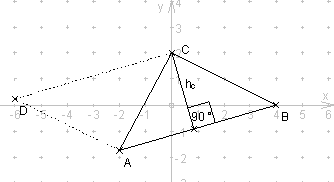, sei .
Berechnung Abstand :
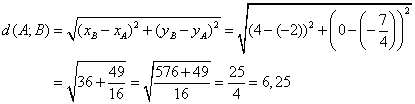
Berechnung Länge :
Umformulierung des Problems: „Abstand des Punktes und dem Schnittpunkt zwischen und .“
Bestimmung Schnittpunkt zwischen und :
Geradengleichung mit Zwei-Punkteform folgt

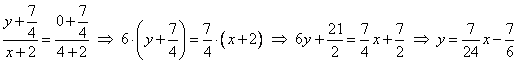
Geradengleichung
Steigung der Geradengleichung : für 2 orthogonale Geraden gilt:
.
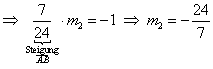mit Punkt-Steigungsform folgt
Schnittpunkt folgt durch gleichsetzen der beiden Geradengleichungen:


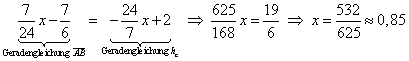
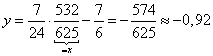
Koordinaten Schnittpunkt
Abstand: 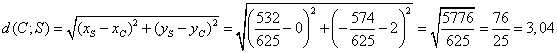FLÄCHENINHALT: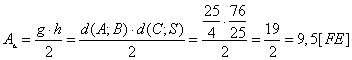

(b) Punkt ist Schnittpunkt der Geraden und .
Bestimmung der Geradengleichung :
und mit dem Punkt folgt:
Geradengleichung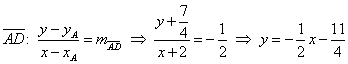
Bestimmung der Geradengleichung :
und mit dem Punkt folgt:
Geradengleichung
Schnittpunkt folgt durch gleichsetzen der beiden Geradengleichungen:


Koordinaten Punkt .

Aufgabe 3:

(a) Wie erkennt man am Schaubild einer Funktion, ob diese eine Umkehrfunktion besitzt?

(b) Gib eine lineare Funktion an, die mit ihrer Umkehrfunktion übereinstimmt.

(c) Wie erkennt man am Graph einer Funktion, dass ist?

Lösung:

(a) Jede Parallele zur -Achse darf das Schaubild höchstens einmal schneiden.

(b) z.B. .

(c) Das Schaubild von ist symmetrisch zur 1. Winkelhalbierenden ().

Aufgabe 4:

Untersuche, ob die Folge sowohl monoton als auch beschränkt ist.

(a)

(b)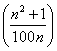

Lösung:

(a) Monotonie: zur Untersuchung bildet man die Differenzenfolge und schätzt das Ergebnis gegenüber ab:
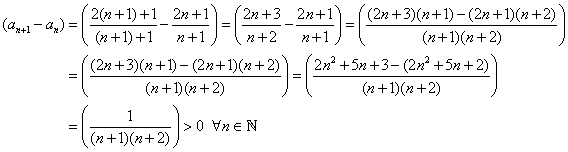
die Folge ist monoton wachsend.

Beschränktheit: Abschätzung der Folge nach oben und unten:
nach unten: da die Folge monoton wachsend für alle ist und so ist eine untere Schranke und es gilt .
nach oben:

Die Folge ist beschränkt, und .

(b) Monotonie: zur Untersuchung bildet man die Differenzenfolge und schätzt das Ergebnis gegenüber ab:

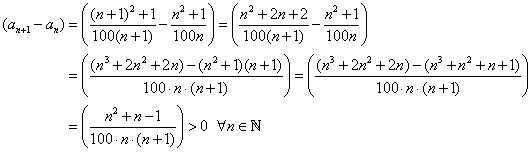
die Folge ist monoton wachsend.

Beschränktheit: Abschätzung der Folge nach oben und unten:
nach unten: da die Folge monoton wachsend für alle ist und so ist eine untere Schranke und es gilt .
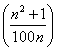nach oben: und ist nach oben unbeschränkt für alle die Folge ist unbeschränkt.

Aufgabe 5:

(a) Bei manchen Folgen ist es zweckmäßig, statt der Differenz den Quotienten zu betrachten. Wie zeigt sich an ihm, dass die Folge monoton ist?

(b) Untersuche mittels des Quotienten die Folgen und auf Monotonie.

Lösung:

(a) Man betrachtet den Quotienten von .
Ist die Folge monoton zunehmend, dann ist das Folgenglied und es gilt:
für
für .
Ist die Folge monoton abnehmend, dann ist das Folgenglied und es gilt:
für
für .

(b) Untersuchung der Folge 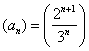auf Monotonie:
es gilt . Für den Quotient gilt:
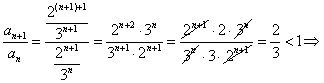monoton abnehmend

Untersuchung der Folge auf Monotonie:
es gilt . Für den Quotient gilt:
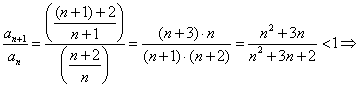monoton abnehmend

Aufgabe 6*:

Beurteile (und begründe) folgende Aussage: „Wenn ein Guthaben sich jährlich um 5% vermehrt, dann vermehrt es sich in 10 Jahren um , also die Hälfte.“

Lösung:

Die Aussage ist falsch, denn es werden die jährlichen Zinsen nicht mit verzinst. („Zinseszins“).