Ana 1:
Gegeben ist die Funktionenschar 
mit
.
(a)
Bestimme für allgemeines 
Nullstellen,
Asymptoten und Punkte mit waagrechten Tangenten.
(b) Führe eine allgemeine Kurvendiskussion durch. Bestimme:
(i) Definitionsmenge
(ii) Symmetrie
(iii) Polstellen, senkrechte Asymptoten
(iv) Verhalten
für 
und 
(v) Nullstellen
(vi) Ableitungen
(vii) Extremstellen
(viii)
Wendestellen
(vergleiche hierzu Buch LS Analysis LK S.177f)
(c)
Zeichne den Graphen von 
im Bereich
.
(d)
* Welche Bedingungen müssen zwei Parameter 
und 
erfüllen, wenn sich
ihre Graphen im Ursprung rechtwinklig schneiden?
Welche Bedingung müssen die beiden Parameter erfüllen, wenn sich ihre Graphen
in dem vom Ursprung verschiedenen Schnittpunkt rechtwinklig schneiden?
Gibt es Graphen, die sich in den beiden Schnittpunkten rechtwinklig schneiden?
*) Aufgabe mit höherem Anpruchsniveau!
LA1:
Gegeben sind die Punkte 
und 
und
die Gerade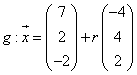 
.
(a)
Die Ebene 
enthält 
und 
. Bestimme die Koordinatengleichung von . (Lösungshinweis: 
)
(b)
Fälle das Lot von auf . Gib die Koordinaten des Lotfußpunktes 
und die Länge 
des Lotes an.
(c)
Bestimme diejenigen Punkte 
und 
auf , die von die Entfernung haben.
(d)
Bestimme die Punkte 
und 
, so dass das Viereck 
ein Quadrat mit dem
Mittelpunkt ist.
(e)
Die Gerade und der Punkt 
bilden die Ebene 
. Bestimme die Koordinatengleichung von .
* Berechne den Schnittwinkel der Ebenen und .
(f)
Über dem Quadrat wird eine senkrechte
Pyramide errichtet, von der eine Seitenfläche in der Ebene liegt. Berechne die
Koordinaten der Spitze 
und das Volumen dieser
Pyramide.
(g)
Bei welcher Wahl von 
als Spitze beträgt das
Volumen der Pyramide bei gleicher Grundfläche 
?
Sockastik1:
Eine Firma stellt Staubsauger her. Bei der Produktion der
Geräte treten unabhängig voneinander die Fehler 
und 
mit den
Wahrscheinlichkeiten 
bzw. 
auf, andere Fehler
werden nicht beobachtet.
Wie groß ist die Wahrscheinlichkeit, dass bei einem Gerät:
(a) beide Fehler auftreten
(b) mindestens ein Fehler
(c) genau ein Fehler
(d) kein Fehler auftritt?
Stochastik2:
In einer Hühnerfarm
werden Eier ausgebrütet. Jedem Ei entschlüpft mit einer
Wahrscheinlichkeit von 
ein
Hühnchen und mit der gleichen Wahrscheinlichkeit ein Hähnchen. Mit der
Restwahrscheinlichkeit von 
liefert das Ei kein
Küken.
Gib einen exakten Term und einen Näherungswert für die Wahrscheinlichkeit an, dass aus 10 Eiern
(a) genau acht Küken
(b) mindestens drei Hähnchen
(c) genau vier Hühnchen und vier Hähnchen ausschlüpfen.
Stochastik3:
Ein Produzent von Kacheln hat erfahrungsgemäß 
Ausschuss, der
zufällig unter den brauchbaren Kacheln verteilt ist. Gib einen exakten Term und
einen Näherungswert für die Wahrscheinlichkeiten an, dass von 20 zufällig
ausgewählten Kacheln
(a) alle brauchbar sind,
(b)
höchstens drei Kacheln Ausschuss sind.