Sei eine gebrochenrationale Funktion mit

.

Hier gehören nur solche -Werte zur Definitionsmenge , für die ist. Hat den Grad , so kann es maximal -Werte geben, für welche nicht definiert ist.

Ist eine Nullstelle des Nenner [], aber für den Zähler gilt :

für .

Man nennt dann eine Polstelle und sagt: Die Funktion hat an der Stelle einen Pol.

Beispiel 1: (Pol mit und ohne Vorzeichenwechsel):

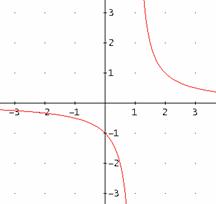
(a) . An der Stelle 1 hat einen Pol.
Für gilt .
für gilt .
Hier: hat Polstelle mit Vorzeichenwechsel
bei 1.

(b)
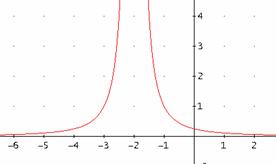
hat an der Stelle einen Pol ohne Vorzeichenwechsel.

(c)
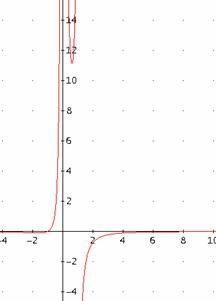
hat zwei Polstellen und .
Pol ohne Vorzeichenwechsel, Pol mit Vorzeichenwechsel.
[Überlegung immer wie im Beispiel 1(a), d.h. „links“ und „rechts“ neben der Polstelle Funktionswerte berechnen und dadurch einen Vorzeichenwechsel erkennen.]

Beispiel 2: (keine Polstelle):

.

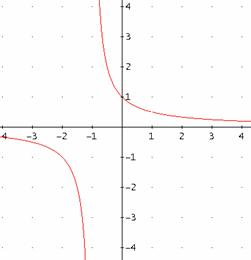
Aber durch kürzen lässt die gebrochenrationale Funktion umschreiben:

mit dem Ausgangsdefintionsbereich .

d.h. an der Stelle hat keinen Pol. Jedoch der gehört der Punkt nicht zum Graph (da ist).

An der Stelle hat einen Pol mit Vorzeichenwechsel.

Lemma (ohne Beweis):

Ist Nullstelle des Nenners und auch des Zählers, lässt sich stets der Linearfaktor im Nenner und Zähler ausklammern (Polynomdivision) und kürzen.

Verhalten einer gebrochenrationalen Funktion für

Anders als bei ganzrationalen Funktionen kann sich das Schaubild einer gebrochenrationalen Funktion dabei zunehmend der -Achse (oder einer anderen Geraden) nähern. Eine solche Gerade heißt Asymptote.

Existiert eine lineare Funktion (=Gerade) , so dass

oder

gilt, so nennt man das Schaubild von eine Asymptote des Schaubildes von .

Daraus folgt: wenn eine Polstelle ist, dann ist die Gerade eine senkrechte Asymptote.

Satz: Das Schaubild einer gebrochenrationalen Funktion mit

hat im Falle:

die -Achse als Asymptote,

die Gerade mit der Gleichung als waagrechte
Asymptote,

eine schiefe Asymptote, die man durch Polynomdivision erhält.