1 Basiswissen:

1.1 Definition: In einer Ebene werden durch ein Koordinatensystem Punkte und Zahlenpaare einander zugeordnet. Ist dem Zahlenpaar der Punkt zugeordnet, so schreiben wir und nennen und die Koordinaten von P.

1.2 Bezeichnung: (lies: Betrag von x) bezeichnet die größere der Zahlen und bzw. , falls .

1.3 Bezeichnung: (lies: Maximum von x und y) bedeutet die größere der Zahlen und , bzw. den gemeinsamen Wert von und , falls .

1.4 Definition: Eine Strecke ist durch ihre Endpunkte und bestimmt. Durch die Koordinaten von und sind also z.B. auch die Länge, die Mitte und die Richtung der Strecke festgelegt.

1.5 Lemma: Die Länge einer Strecke wird in der Längeneinheit angegeben, welche auf den Koordinatenachsen gegeben ist. Nach dem Satz des Pythagoras gilt:
.
(Bemerkung: Für die Berechnung der Länge der Strecke ist die Reihenfolge der Punkte irrelevant, wie der Leser leicht erkennt.)

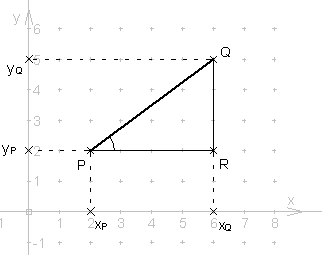
1.6 Lemma: Die Richtung einer Strecke ist festgelegt durch den Winkel , den sie mit der Richtung der positiven x-Achse bildet.

Ist eine Strecke durch die Koordinaten von und gegeben, so verwendet man statt den leichter zu berechnenden Tangens von , also das Verhältnis .

Die Zahl heißt Steigung ( Steigungswinkel) von und wird mit bezeichnet. Falls ist, gilt:
.
Ist , also parallel zur y-Achse, so ist ; solche Strecken haben keine Steigung(szahl).
(Bemerkung: Für die Berechnung der Steigung einer Strecke ist die Reihenfolge der Punkte irrelevant, wie der Leser leicht erkennt.)

1.7 Lemma: Für die Mitte von gilt:
.

1.8 Lemma: Sei eine Gerade. Jedes Zahlenpaar mit erfüllt die Gleichung (Hauptform).
Für achsenparallel Geraden durch gilt:
Parallele zur y- Achse: ,
Parallele zur x-Achse: .

1.9 Satz: Ist eine Gerade gegeben durch einen Punkt und die Steigung oder durch zwei Punkte , , so erhält man ihre Gleichung aus
, bzw. .

1.10 Satz: Jede Gleichung der Form

stellt in der -Ebene eine Gerade dar.

1.11 Lemma: Geraden mit den Steigungen und sind genau dann parallel, wenn gilt:

1.12 Lemma: Geraden mit den Steigungen und sind genau dann orthogonal, wenn gilt:
.

1.13 Lemma: Zwei sich schneidende Geraden und bilden (sofern sie nicht orthogonal sind) zwei Winkel. Den kleineren der beiden nennen wir den Schnittwinkel von und . Um (mit ) zu berechnen, ermitteln wir aus den Steigungen und die Steigungswinkel und . Ist , so gilt
.

1.14 Definition: Eine Zuordnung der Form heißt lineare Funktion.

1.15 Satz: Bei einer linearen Funktion gilt für jeden -Wert: Vergrößert man den -Wert um , so ändert sich der Funktionswert um das -fache von .

1.16 Definition: Lineare Funktionen der Form heißen Proportionalitäten (proportionale Funktionen).

1.17 Definition: Zuordnungen der Form heißen Potenzfunktionen.

1.18 Satz: Bei einer Funktion wird dem -fachen eines -Wertes das -fache seines Funktionswertes zugeordnet.

1.19 Definition: Zuordnungen der Form heißen Exponentialfunktionen.

1.20 Satz: Wenn man bei Funktionen der Form zu einem -Wert addiert, dann wird der zugehörige Funktionswert mit multipliziert.

1.21 Definition: Unter dem Bogenmaß eines Winkels versteht man die Maßzahl der zugehörigen Bogenlänge im Einheitskreis.
Bsp.: Gradmaß: = Bogenmaß ; Gradmaß: = Bogenmaß , …

1.22 Definition: und .

1.23 Definition: Die Zuordnung heißt Sinusfunktion und die Zuordnung heißt Kosinusfunktion.

1.24 Satz: Es ist und für alle . Die Sinus- und die Kosinusfunktion sind periodisch mit der Periode , d.h.
und für alle ,
und für alle .

1.25 Lemma: Additionstheoreme

1.26 Definition: sei eine nichtleere Teilmenge von . Eine Zuordnung, die jeder Zahl genau eine reelle Zahl zuordnet, heißt (reelle) Funktion.
Wenn eine Zuordnungsvorschrift jedem dieselbe Zahl zuordnet wie eine Zuordnungsvorschrift , so sagen wir: und bestimmen dieselbe Funktion.

1.27 Definition: Eine Funktion mit , , deren Funktionsterm ein Polynom ist oder auf diese Form gebracht werden kann, heißt ganzrationale Funktion n-ten Grades. Das Schaubild von heißt (für ) Parabel n-ter Ordnung.

1.28 Definition: sei eine umkehrbar eindeutige Funktion. Dann heißt die Funktion
mit
die Umkehrfunktion von .

1.29 Satz: Die Funktion hat für die Umkehrfunktion .

1.30 Satz: Die Exponentialfunktion hat die Umkehrfunktion
.
Ihre Definitionsmenge ist , ihre Wertemenge .

2 Grenzwerte

2.1 Bemerkung: Eine Zahlenfolge kann einen „Grenzwert“, eine Folge von Figuren eine „Grenzfigur“, eine Folge von Punkten einen „Grenzpunkt“ haben. Die Vermutung, dass eine unendliche Folge von immer größer werdenden Zahlen schließlich jede noch so große Zahl überschreitet, ist nicht richtig.

2.2 Definition: Eine Zahlenfolge heißt
monoton zunehmend (oder monoton steigend), wenn für alle ,
monoton abnehmend (oder monoton fallend), wenn für alle .

2.3 Definition: Eine monotone Folge heißt nach oben beschränkt, wenn es eine Zahl gibt, so dass ist für alle . Eine monotone Folge heißt nach unten beschränkt, wenn es eine Zahl gibt, so dass ist für alle . nennt man obere Schranke, eine untere Schranke der Folge.

2.4 Bemerkung: Die Begriffe „obere Schranke“ und „untere Schranke“ verwendet man in gleicher Weise bei nicht-monotonen Folgen. Hat eine Folge sowohl obere als auch untere Schranken, so nennt man sie kurz eine beschränkte Folge.